废话
因为四月份的蓝桥杯省赛拿了省一等奖,也报了国赛,加上6月2号的ACM,所以在这段时间里面要搞搞算法。
这段时间的面试(只面了京东(校招)和头条(内推)),暴露出来的是Java基础了解的不够深入,同时算法一直以来都是我的薄弱环节,希望这两个比赛能够让我得到一点提升。
这篇文章是为了我能够记住解题的思想同时也算是整理一下思路。
什么是LCS
LCS(Longest Common Subsequence)——最长公共子序列
定义
一个序列S任意删除若干个字符得到新序列T,则T叫做S的子序列。
两个序列X和Y的公共子序列中,长度最长的那个,定义为X和Y的最长公共子序列。
这里主要区分一下子序列和子串(最长公共子序列和最长公共子串),最长公共字串要求连续
字符串 “13455” 与 “245576” 的最长公共子序列为“455”。
字符串“acdfg”与“adfc”的最长公共子序列为“adf”。
LCS的意义
主要运用于比对的地方,比如图形的相似处理、媒体流的相似比较等。生物学家常常利用该算法景象基因序列比对,由此推测序列的结构、功能和演化过程。
LCS可以用来描述两段文字之间的“相似度”,即它们的雷同程度,从而能够用来判断抄袭。另一方面,对一段文字进行修改之后,计算改动前后文字的最长公共子序列,将除此子序列外的部分提取出来,这种方法判断修改的部分,往往十分准确。
求解——暴力法
最简单的想法便是列出字符串X的所有子序列,同时列出字符串Y的所有子序列,然后求出这两个字符串的所有子序列相同且最长的一个,便是最长公共子序列。
加入字符串X的长度是m,字符串Y的长度是n,那么X共有\(2^m\)个不同子序列,Y有\(2^n\)个不同子序列,同时进行遍历,那么时间复杂度为O(\(2^m*2^n\))。
显然,这是不可取的。
LCS解法探索
在这里,我们先做几个定义:
假定字符串X,长度为m,从1开始数;
假定字符串Y,长度为n,从1开始数;
Xi=<x1,x2,···,xi>即X序列的前i个字符(1<i<m);
Yj=<y1,y2,···,yj>即Y序列的前j个字符(1<j<n>);
LCS(X,Y)为字符串X和Y的最长公共子序列,即Z=<z1,z2,···,zk>;
事实上,X和Y的可能存在多个子串,长度相同并且最大,因此,LCS(X,Y)严格的说,是个字符串集合。即:Z∈ LCS(X , Y)
在这里我们进行如下分析:
第一种情况:\(x_m=y_n\)(最后一个字符相同)
则:\(X_m\)与\(Y_n\)的最长公共子序列\(Z_k\)的最后一个字符必定是\(X_m\)(\(Y_n\));
此时,\(Z_k\)=\(X_m\)=\(Y_n\)
LCS(\(X_m\),\(Y_n\))=LCS(\(X_{m-1}\),\(Y_{n-1}\))+\(X_m\)
举例:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| X | B | D | C | A | B | A | |
| Y | A | B | C | B | D | A | B |
对于上面的字符串X和Y,
\(x_3=y_3\)=’C’,则:LCS(BDC,ABC)=LCS(BD,AB)+‘C’
\(x_5=y_4\)=’B’,则:LCS(BDCAB,ABCB)=LCS(BDCA,ABC)+‘B’
第二种情况:\(x_m{\ne}y_n\)
此时又分为两种情况:
- LCS(\(X_m\),\(Y_n\))=LCS(\(X_{m-1}\), \(Y_n\))
- LCS(\(X_m\),\(Y_n\))=LCS(\(X_m\), \(Y_{n-1}\))
证明:
令\(Z_k\)=LCS(\(X_m\),\(Y_n\));
由于\(x_m{\ne}y_n\),则\(z_k{\ne}x_m\)与\(z_k{\ne}y_n\)至少有一个必然成立,不妨假定\(z_k{\ne}x_m\)(\(z_k{\ne}y_n\)的分析与之类似)。因为\(z_k{\ne}x_m\),则最长公共子序列\(Z_k\)是\(X_{m-1}\)和\(Y_n\)得到的,即: \(Z_k\)=LCS(\(X_{m-1}\), \(Y_n\))同理,若\(z_k{\ne}y_n\),则\(Z_k\)=LCS(\(X_m\), \(Y_{n-1}\))
即:若\(x_m{\ne}y_n\),则:
LCS(\(X_m\),\(Y_n\))= max{LCS(\(X_{m-1}\), \(Y_n\)),LCS(\(X_m\), \(Y_{n-1}\))}
举例:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| X | B | D | C | A | B | A | |
| Y | A | B | C | B | D | A | B |
对于字符串X和字符串Y:
\(x_2{/ne}y_2\),则:LCS(BD,AB)=max{ LCS(BD,A), LCS(B, AB) }
\(x_4{/ne}y_5\),则:LCS(BDCA,ABCBD)=max{ LCS(BDCA,ABCB), LCS(BDC,ABCBD) }
因此:
编码实现
我们使用一个二位数组用来C[m,n]来存储子序列的长度,c[i,j]记录了\(X_i\)和\(Y_j\)的最长公共子序列的长度。
当i=0或者j=0是,空序列是\(X_i\)和\(Y_j\)的最长公共子序列,故c[i,j]=0。
使用另一个二维数组B[m,n],用于标记c[i,j]的值是由哪个子问题的解得到的。即c[i,j]是由c[i-1,j-1]+1或者c[i-1,j]或者c[i,j-1]的哪一个得到的。取值范围为Left、Top、LeftTop三种情况。
举例:
X=< A,B,C,B,D,A,B >
Y=< B,D,C,A,B,A >
最终得到的两个二维数组如图所示: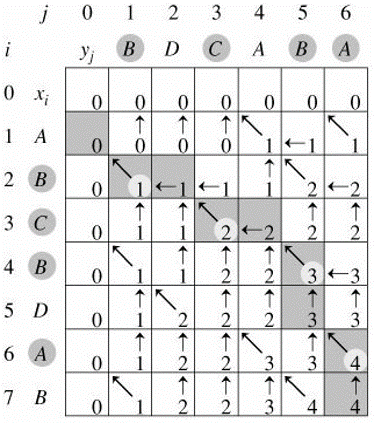
1 | public class LCS { |
在这里,lcs()返回的是最长的公共子序列,但是我没有做处理,此时返回的字符串是反向的,因为我们最后在通过方向数组寻找子序列的时候,是从后往前,所以这里的字符串是反向的。
在这里给出伪代码实现:


说在后面
在这里,这个算法依旧可以继续优化,但是由于我还没有搞清楚优化的原理,所以暂时不写,如果有需要的可以查看参考链接获取更多信息。

